Robot Motion Planning in High-Dimensional Environments
High-dimensional motion planning addresses the computational challenges that arise when robots possess many degrees of freedom. A humanoid robot with dozens of joints, a multi-arm manipulation system, or coordinated multi-robot teams create configuration spaces with tens or hundreds of dimensions. Traditional planning approaches that work well in two or three dimensions become computationally intractable in high-dimensional spaces due to exponential growth in the volume that must be searched. Advanced techniques including sampling-based algorithms, dimensionality reduction, and learned motion primitives enable planners to find solutions efficiently while maintaining collision-free operation and satisfying task-specific constraints.
Sampling-Based Planning Techniques
Probabilistic roadmaps and rapidly-exploring random trees represent the most successful approaches for high-dimensional planning. These algorithms avoid explicit space discretization by randomly sampling configurations and building connectivity graphs that capture the structure of collision-free space.
- RRT algorithms efficiently explore high-dimensional spaces by incrementally growing trees toward randomly sampled goals
- PRM methods build reusable roadmaps through preprocessing that answer multiple queries efficiently
- Bidirectional search variants grow trees from both start and goal configurations to accelerate solution discovery
- Optimal variants like RRT-star asymptotically converge to minimum-cost solutions through continuous path refinement

Computational Complexity Comparison
Algorithm performance varies significantly based on problem dimensionality and environmental complexity:
| Dimensions | Grid-Based Time | Sampling-Based Time |
|---|---|---|
| 2-3 DOF | 10-100ms | 20-200ms |
| 6-7 DOF | 10-60 seconds | 100-500ms |
| 12+ DOF | Intractable | 500ms-5 seconds |
| Coordinated Teams | Intractable | 1-30 seconds |
"Sampling-based approaches have revolutionized high-dimensional motion planning by providing probabilistic completeness guarantees while remaining computationally tractable for systems with dozens of degrees of freedom."
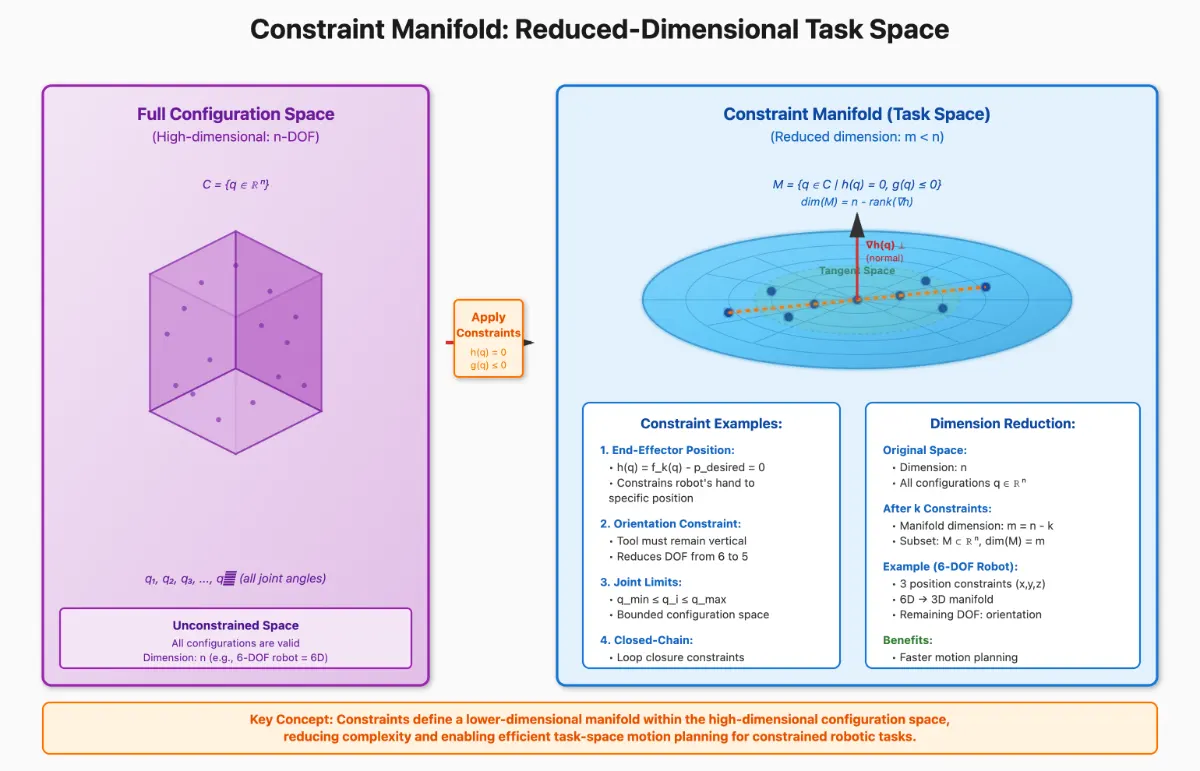
Dimensionality Reduction Strategies
Reducing effective problem dimensionality through task space decomposition, constraint manifold identification, and motion primitive libraries significantly improves planning efficiency. These techniques identify lower-dimensional subspaces where task-relevant motion occurs, allowing planners to focus computational resources on the dimensions that actually matter for successful task completion while treating other dimensions as constrained or less critical to the planning objective.